幾何原本－科學第一聖經的秘密

Last Updated on 2022-05-18 by 明心

《幾何原本》（Στοιχεῖα，Stoicheia，Elements），文明暢銷書總榜單無敵暢銷書，連續300年長踞暢銷榜第一，連續2000年長踞暢銷榜第二，在今日卻罕為人知的曠世巨著。

• 哲學、數學、物理、科學、文明聯合強力推薦！！
• 《世界暢銷書 Top 10》，雄踞排行榜超過154451天！！！
• 笛卡兒、牛頓、歐拉、高斯、愛因斯坦等人衷心推薦。
• 入選文明影響力指南，被評為「撬動世界的槓桿」。

這本書從何而來？憑什麼如此暢銷？今日的沒沒無聞，又在提醒著我們什麼？

就讓我們一一揭曉！

延伸閱讀：笛卡兒的生命歷程：從玫瑰十字會到被你誤解的我思故我在

名字都很像的古希臘哲學家

在剛開始接觸古希臘文明時，我自己常搞混古希臘哲學家的名字，為了避免你有同樣的困惑，先做個簡單釐清：

• 亞歷山卓的歐幾里得（Euclid）：今天的主角，詳情後續。
• 阿基米德（Archimedes）：辨識真假皇冠、用棍子撬地球的裸奔愛好者。
• 亞里斯多德（Aristotle）：柏拉圖的弟子，亞歷山大大帝的老師，牛頓出道前，西方知識體系最具影響力的人物之一。
• 墨伽拉的歐幾里得（Euclid of Megara）：古希臘哲學家，以「自稱正撒謊者能否講真話」悖論著名。

關於咱們這本「暢銷書」的作者歐幾里得，事實上我們所知不多。生足年不詳，大概活了60歲，有著作《幾何原本》，人們常常把他和墨伽拉的歐幾里得搞混。

他可能在雅典北方的柏拉圖學院學習過，一生中大半的時間，都待在埃及亞歷山卓圖書館。

亞歷山卓圖書館

伯羅奔尼薩戰爭結束後，馬其頓趁著希臘政權分裂，輕易地攻陷了雅典。亞歷山大大帝繼承馬其頓王位後，開始他征服世界的旅程，並挑選眾多軍事要地建立一座座城市。

西元前332年，亞歷山大佔領埃及後，在距今開羅西北200公里處，聘請最好的建築師，親自監工、規劃移民，建立了一座以自己名字為名的都市，這座城市便是亞歷山卓。

九年後，年僅32歲的亞歷山大遠征完印度，在巴比倫暴斃。帝國一分為三，其中埃及的托勒密王朝，在托勒密一世（Ptolemy I）統治時定都亞歷山卓，並建立了當時世界最大的圖書館，據說藏有60萬卷紙草書。

自此，亞歷山卓便成為希臘民族文化、精神的象徵，也被稱為地中海的珍珠。

而歐幾里得便是在這樣的環境中，統整柏拉圖、米利都的泰勒斯（Thales）、畢達哥拉斯（Pythagoras）等人的理念，將其整理成《幾何原本》，日後阿基米德也是在此，向歐幾里得的弟子進行學習相關的知識。

教你如何高EQ應對無理的上司

據說，托勒密一世曾詢問歐幾里得：「噢～幾何學好多又好難呀！有沒有什麼簡單快速的方法，我可以多付點錢。」

高EQ的歐幾里得回應：「幾何無王者之道。」（There is no royal road to geometry.）

低EQ的歐幾里得偷偷地罵：「想偷懶，食屎啦你！」（No Way!）

延伸閱讀：五個問題，檢視羊群效應與你的盲從程度

《幾何原本》

幾何原本共分為13卷，分別探討平面幾何、立體幾何與數論，但這本書最精華的部分，並非在探討的內容，而是這本書背後蘊藏的思維概念。

並非原創的經典

事實上，書中關於數論、幾何的定理，乃至於相關的證明方法，早在歐幾里得之前就為人所知，例如國中時讓你頭昏腦脹的畢氏定理。

歐幾里得所做的，是將其做了系統性的整理，讓其依循嚴謹的邏輯架構，從無到有的，一步、一步地建構出幾何大廈。

你或許還是十分困惑，這樣做感覺沒什麼了不起呀？

就讓我們用幾何原本來說明吧！

可以同時搭配：線上互動式全彩英文版的幾何原本《The Elements of Euclid》

並非理所當然的理所當然

平面三角形的內角和為什麼是180°？等腰三角形的兩個底角為什麼相等？

可能一些對數學還有記憶的人會說：「噢！可以用平行線的內錯角相等、三角形全等來證明……」

但問題又來了，那為什麼平行線的內錯角會相等、三角形有全等性質……？

這樣不斷地問、不斷地問，那最初的源頭是什麼？

只能從源頭出發

歐幾里得在整理中，提出了23個定義（Definitions）、5個公設（Postulates）、5個公理（Axioms），這是他認為的源頭：

• 定義：一件事物基礎屬性的描述、說明。
• 公設：從經驗中，總結出的幾何學常識、事實。
• 公理：顯而易見、不證自明的斷言。

而所有的命題（不確定是否正確、可能正確的問題），都必須藉由定義、公設、公理去建構，經過證明才能成為所謂的定理。

反過來說，如果不是出自於定義、公設、公理的部分，都是不被允許的！

那麼，歐幾里得的定義、公設、公理是什麼呢？

你可以在閱讀的同時，仔細地看看有沒有那個定義、公設、公理是不夠基本、可以再往根源處追問的？

23個定義

1. A point is that which has no part.（點是沒有部分的）
2. A line is breadthless length.（線只有長度、沒有寬度）
3. The ends of a line are points.（一條線的兩端是點）
4. A straight line is a line which lies evenly with the points on itself.（一條直線是沿一定方向，及其反方向的點所鋪成）
5. A surface is that which has length and breadth only.（面只有長度和寬度）
6. The edges of a surface are lines.（一個面的邊緣是線）
7. A plane surface is a surface which lies evenly with the straight lines on itself.（平面是直線自身的均勻分布）
8. A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.（平面角，是在一平面內兩條直線相交，所形成的傾斜程度）
9. And when the lines containing the angle are straight, the angle is called rectilinear.（當平面角的角度是筆直時，則為平角180°）
10. When a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.（當一直線站立於另一條直線，使得形成的角度，相等於形成的另一角度，則兩個角度都可以稱為直角90°，而其中一條線可稱為另一條直線的垂線）
11. An obtuse angle is an angle greater than a right angle.（鈍角是大於直角的角）
12. An acute angle is an angle less than a right angle.（銳角是小於直角的角）
13. A boundary is that which is an extremity of anything.（邊界是事物之邊緣）
14. A figure is that which is contained by any boundary or boundaries.（圖是由一個或多個邊界所構成）
15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure equal one another.（圓是由一條線包圍著的平面圖形，內部有一點，與這條線上任何一點，所連成的線段都相等）
16. And the point is called the center of the circle.（此點為圓心）
17. A diameter of the circle is any straight line drawn through the center and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.（直徑是通過圓心，且端點在圓上的任意線段，該線段將圓分成兩等分）
18. A semicircle is the figure contained by the diameter and the circumference cut off by it. And the center of the semicircle is the same as that of the circle.（半圓是直徑，和被它所切割的圓弧，所形成的圖形。半圓之圓心和原本之圓心相同）
19. Rectilinear figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.（直線圖形，是由線段首尾-首尾相連，所形成的圖形。三角形由三條線段所圍成，四邊形由四條線段所圍成，多邊形由四條以上的線段所圍成）
20. Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.（三角形中，三條邊相等之三角形為正三角形，兩條邊相等的為等腰三角形，各邊都不相等的為不等邊三角形）
21. Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute.（此外，三角形中有一個直角的為直角三角形，有一個角是鈍角的為鈍角三角形，三個角都是銳角的為銳角三角形）
22. Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.（在四邊形中，四個邊相等，且四個角都是直角的為正方形；四個角是直角，但四個邊不完全相等的是矩形；四個邊相等，角不是直角的為菱形；兩組對邊、兩組對角分別相等的，是平行四邊形；一組對邊平行、一組對邊不平行的，為梯形）
23. Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.（平行直線，是在同一平面，向兩個方向無限延長，卻無法相交的直線）

5個公設

• To draw a straight line from any point to any point.（從一點向另一點可引一條直線）
• To produce a finite straight line continuously in a straight line.（任意線段能無限延伸成一條直線）
• To describe a circle with any center and radius.（給定任意線段，可以以其一個端點作為圓心，該線段作為半徑作一個圓）
• That all right angles equal one another.（所有直角都相等）
• That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. （若兩條直線都與第三條直線相交，並且在同一邊的內角之和小於兩個直角，則這兩條直線在這一邊必定相交）

備註：這五大公設同時也是「尺規作圖」的基石，也就是作圖時只能使用沒有刻度的直尺、圓規、必須在有限步驟內完成作圖。

備註2：第五條公設稱為平行公設（Parallel Axiom），可以導出下述命題：通過一個不在直線上的點，有且僅有一條不與該直線相交的直線。這個定理在數千年後，挑戰了人們對於「真理」的觀點。

延伸閱讀：標準答案，是謊言還是真相？

5個公理

• Things which equal the same thing also equal one another.（與同一事物相等的事物相等，即若A=B且B=C，則A=C）
• If equals are added to equals, then the wholes are equal.（相等的事物加上相等的事物仍然相等，即若A=B，則A+C=B+C）
• If equals are subtracted from equals, then the remainders are equal.（相等的事物減去相等的事物仍相等，即若A=B，則A-C=B-C）
• Things which coincide with one another equal one another.（一個事物與另一事物重合，則它們相等）
• The whole is greater than the part. （整體大於局部）

命題I.1

看完之後，有沒有感覺很像廢話呢？為什麼要花這麼大的篇幅，來記錄這些「顯而易見」的事物？

我們來看看幾何原本中，第一卷的第1個命題吧。

命題1：給定一個有限線段（為邊），做一個正三角形。

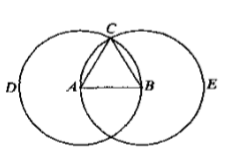
假設AB為有限線段，要以AB線段作為正三角形的一邊，作一個正三角形。

方法：

1. 以A為圓心，以AB為半徑畫圓BCD（根據：公設3）
2. 以B為圓心，以BA為半徑畫圓ACE（根據：公設3）
3. 從兩圓的交點C，連結點A、C，畫出CA、CB。（根據：公設1）
4. 由於點A是圓BCD的圓心，所以AC=AB。（根據：定義15）
5. 由於點B是圓ACE的圓心，所以BC=AB。（根據：定義15）
6. 由於AC=AB且BC=AB，所以AC=BC。（根據：公理1）

完成命題。

聰明的你，應該已經發現關鍵：每一個步驟，都必須有源自定義、公設或公理的依據。

但如果是這樣，那較為複雜的證明不就得一本書了？關於這點，我們便用命題2來說明吧～！

命題I.2

命題2：由一個已知點（作為端點），作一線段等於已知線段。

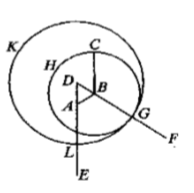
假設A是已知點，BC是已知線段，要作一線段和BC等長（而且A是端點）。

方法：

1. 連點A和點B，成為線段AB。（根據：公設1）
2. 以有限線段AB為一邊，做一個正三角形ABD。（根據：命題1）
3. 延長DA成為直線DE，延長直線DB成為直線DF。（根據：公設2）
4. 以B為圓心，BC為半徑畫圓CGH。（根據：公設3）
5. 以D為圓心，DG為半徑畫圓GKL。（根據：公設3）
6. 由於點B是圓CGH的圓心，所以BC=BG。（根據：定義15）
7. 由於點D是圓GKL的圓心，所以DL=DG。（根據：定義15）
8. 同時因為DA=DB，所以AL=BG。（根據：公理3）
9. 由6可知，BC=BG，所以AL、BC皆等於BG。（根據：公理1）

完成命題。

延伸閱讀：科學是什麼，可信嗎－你所認為的正確與真實，究竟是「什麼」？

幾何原本最重要的精神

是的，建構於「簡單到像是廢話」的定義、公設、公理，以及此前完成的命題，歐幾里得一步一步、從無到有的完全了證明。

每一個步驟都是如此的嚴謹，秩序與清晰，人們可以確信他所走的每一步都是「正確的」。這樣的信念與思想，被日後天主教中的耶穌會所認同，還拯救了即將分崩離析的羅馬教廷，這又是另外一段故事了。

很遺憾的是，我們今日的教育鮮少提及《幾何原本》背後的精神，反倒著重在其中的命題、解法，成為國小、國中的教學內容，這是十分可惜的事情。

若是學生能深刻的經驗數學之美，這樣的教育才是具有生命力的教育。

延伸閱讀：感動的教育，關鍵是……

---

如果覺得文章還不錯，歡迎和好友「分享」，下面按讚的按鈕，用力點五下可以「免費」的幫助我（需註冊），感謝你！！

或者如果你願意，可以「贊助我一杯咖啡♨」，你的支持是我書寫文章最大的動力之一。

小聲的說，其實右方與下方的網站也都不賴，你也可以參考呦～(灬ºωº灬)